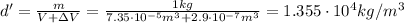Question

The density of Mercury is 1.36 × 10 by 4 Kgm - 3 at 0 degrees. Calculate its value at 100 degrees and at 22 degrees. Take cubic expansivity of mercury as equal to 180 × 10-6 K -1

Answer 1

D= 1.34*10^4kg/m^3 when t =100c

D=1.36*10^4kg/m^3 when t= 22c

Answer 2

a) Density at 100 degrees:
`1.34\cdot 10^4 kg/m^3`

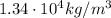
Step-by-step explanation:

The density of mercury at 0 degrees is
`d=1.36\cdot 10^4 kg/m^3`

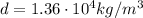
Let's take 1 kg of mercury. Its volume at 0 degrees is

`V=(m)/(d)=(1 kg)/(1.36\cdot 10^4 kg/m^3)=7.35\cdot 10^(-5) m^3`

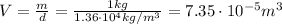
The formula to calculate the volumetric expansion of the mercury is:

`\Delta V= \alpha V \Delta T`

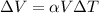
where

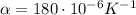`\alpha=180\cdot 10^(-6) K^(-1)` is the cubic expansivity of mercury

V is the initial volume

`\Delta T` is the increase in temperature

In this part of the problem,
`\Delta T=100 C-0 C=100 C=100 K`

So, the expansion is

`\Delta V= \alpha V \Delta T=(180\cdot 10^(-6) K^(-1))(7.35\cdot 10^(-5) m^3)(100 K)=1.3\cdot 10^(-6) m^3`

So, the new density is

`d'=(m)/(V+\Delta V)=(1 kg)/(7.35\cdot 10^(-5) m^3+1.3\cdot 10^(-6) m^3)=1.34\cdot 10^4 kg/m^3`

b) Density at 22 degrees:
`1.355\cdot 10^4 kg/m^3`

We can apply the same formula we used before, the only difference here is that the increase in temperature is

`\Delta T=22 C-0 C=22 C=22 K`

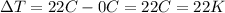
And the volumetric expansion is

`\Delta V= \alpha V \Delta T=(180\cdot 10^(-6) K^(-1))(7.35\cdot 10^(-5) m^3)(22 K)=2.9\cdot 10^(-7) m^3`

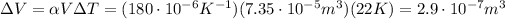
So, the new density is

`d'=(m)/(V+\Delta V)=(1 kg)/(7.35\cdot 10^(-5) m^3+2.9\cdot 10^(-7) m^3)=1.355\cdot 10^4 kg/m^3`