Answer : The standard reduction potential,
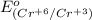 is -0.13 V.
is -0.13 V.
Solution : Given,
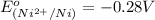
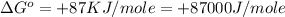 (1 KJ = 1000 J)
(1 KJ = 1000 J)
The net reaction is,
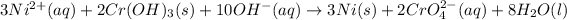
The half cell reactions are :
At cathode :
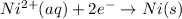
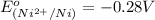
At anode :
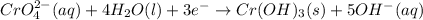
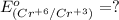
First we have to calculate the
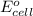 by using formula,
by using formula,
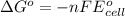
where,
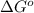 = Gibbs's free energy
= Gibbs's free energy
n = number of electrons in a net chemical reaction = 6 electrons
F = Faraday constant = 96485 C
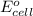 = standard cell potential
= standard cell potential
Now put all the given values in this formula, we get
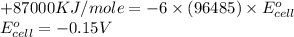
Now we have to calculate the
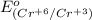 by using formula,
by using formula,
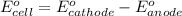
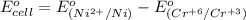
Now put all the given values in this formula, we get
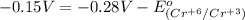
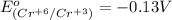
Therefore, the standard reduction potential,
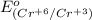 is -0.13 V.
is -0.13 V.