Correct answer is RQ=9
Solution:-
Given that in a ΔPQR, m∠R=90°, MP=18, m∠PQR=75° and m∠MQR=60°.
Since m∠MQR<m∠PQR, M should lie on PR only, Please refer the diagram attached for reference.
From the diagram∠PQM=∠PQR-∠MQR=75°-16°=15°
And in ΔPQR,∠RPQ=180-(remaining 2 angles in triangle)
=180-(90+75)=15°
So, in ΔPQM, ∠MPQ=∠PQM hence the opposite sides must be equal that is
MP=MQ but given MP=18
Hence MQ=18
In ΔMRQ, cos(∠MQR)=
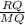
cos(60°)=
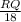
RQ= 18cos(60°)=18X0.5 =9
Hence RQ=9