Question

Write an equation of the line that passes through (4,−1) and is parallel to the line y=3x+7. (hint: NOT y=3x-13)

Answer 1

To find the equation of the line, we are going to use the point-slope form, which is listed below:

`(y - y_1) = m(x - x_1)`

• 
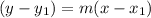
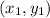  `(x_1, y_1)` is a point on the line
• 
  `m` is the slope of the line

You may notice that we have a point, but no slope is given to us. However, the problem states that the line is parallel to the equation
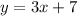`y = 3x + 7`, which means that it has the same slope as this line, which is 3. (Remember that this line is set up in
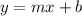`y = mx + b` form, where
`m` is the slope)

Thus, we can now insert our values into the point-slope formula to find the equation of our line.

`(y + 1) = 3(x - 4)`

`(y + 1) = 3x - 12`

`y = 3x - 13`

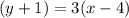
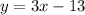
The problem made it clear that it didn't want the form
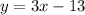`y = 3x - 13`, so let's put it in standard form:

`y = 3x - 13`

`3x - y = 13`

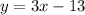
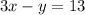
The equation of our line is
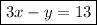`\boxed{3x - y = 13}`.