Question

Help !!!
See question in image.
Please show workings .
​

Answer 1

see explanation

Explanation:

Given f(x) then the derivative f'(x) from first principles is

f'(x) = lim ( h tends to 0 )
`(f(x+h)-f(x))/(h)`

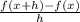
= lim ( h to 0 )
`(3(x+h)^3+2-(3x^3+2))/(h)`

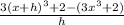
= lim ( h to 0 )
`(3(x^3+3x^2h+3xh^2+h^3)+2-3x^3-2)/(h)`

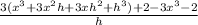
= lim ( h to 0 )
`(3x^3+9x^2h+9xh^2+3h^3-3x^3)/(h)`

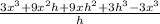
= lim ( h to 0 )
`(9x^2h+9xh^2+3h^3)/(h)`

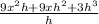
= lim ( h to 0 )
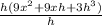`(h(9x^2+9xh+3h^3))/(h)` ← cancel h on numerator/ denominator

= lim ( h to 0 ) 9x²+9xh+3h² ← let h go to zero

f'(x) = 9x²