Question

What is the value of x?

a. x= 3
b. x=18
c. x=30
d. x=9

find JM in the previous item.
A. jm=3
B. jm=9
C. jm=54
D. jm=63

Answer 1

so the triangle is shown that these two triangles are congruent. so you set the equation on both sides

9x-18 = 3x

-18 = -6x

x = 3

now that you know x you plug into the equation of JM

Answer 2

Answer: x=3 and JM=9 units

Explanation:

Given:
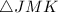`\triangle{JMK}` in which BM is a perpendicular bisector of JK such that JB=BK and
`\angle{JBM}=\angle{KBM}`.

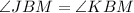Now in
`\triangle{JMB}\ and \triangle{KBM}`

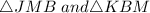
JB=BK [given]

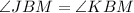`\angle{JBM}=\angle{KBM}` [right angle]

MB=MB [reflexive property]

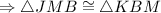`\Rightarrow\triangle{JMB}\cong\triangle{KBM}` [by SAS postulate of congruence]

⇒MJ=MK

`\Rightarrow9x-18=3x\\\Rightarrow9x-3x=18\\\Rightarrow6x=18\\\Rightarrow\ x=3`

Thus JM=
`9(3)-18=27-18=9`

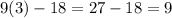
Hence, x=3 and JM=9 units