Answer:
see explanation
Explanation:
Given f(x) then the derivative f'(x) is
f'(x) = lim(h tends to 0 )
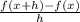
= lim ( h to 0 )
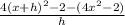
= lim ( h to 0 )
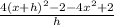
= lim( h to 0 )
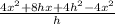
= lim( h to 0 )
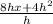
= lim ( h to 0 )
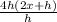 ← cancel h on numerator/ denominator
← cancel h on numerator/ denominator
= lim ( h to 0 ) 4(2x + h) ← let h go to zero
f'(x) = 8x