Question

How many discontinuities does the piecewise function have.?

Answer 1

Answer is 3.

The function is not continuous at the points

x=-3: x=3 and x = 5

Step-by-step explanation:

Consider the left and right limits of the funciton at these points.

i) x=-3

Left limit =
`3e^(-3+3)+1 = 4`

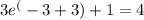
right limit = [/tex]2/3 (9)-1 = 5[/tex]

Since left limit not equals right limit not continuous at x =-3

ii) x=3

Left limit = 5 and right limit = -7(3)/2+29/2 = 4

Since left limit not equals right limit not continuous at x =3

iii) x=5

Left limit = 7(5)/2+29/2 = 32

Right limit = log (2*5-4) = log 6

Since left limit not equals right limit not continuous at x =5.

Thus there are 3 discontinuities.

Answer 2

In piecewise linear functions, the endpoint of one segment and the initial point of the next segment can have the same x-coordinate but a different value of f(x).

Such difference in values is called a step or discontinuity and such a function is called a discontinuous function.

Here in this case, there are 3 discontinuities: x=-3, x=3 and x = 5.

x = -3 because x is smaller than or greater than -3 but not equal.

x = 3 since greater than 3 in one of the inequalities.

x = 5 since x is smaller than 5 in one of the limits.