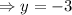Answer-
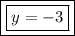
Solution-
The two points given here are (-2,-3) and (3,-3).
We can derive the straight line equation between these two points by applying two points formula.
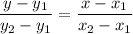
Here,
x₁ = -2
y₁ = -3
x₂ = 3
y₂ = -3
Putting the values,
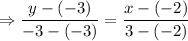
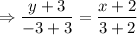
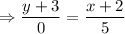
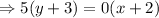
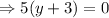
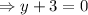
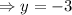
Therefore, the equation of the line is