Answer:
Given: Vertex (3,5) and focus (3,9) of the parabola.
As you can see that the x-coordinates of the vertex and focus are the same, so, this is a regular vertical parabola.
The Standard form of the equation of the parabola is;
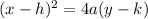 , where a≠0. ......[1]
, where a≠0. ......[1]
The vertex of this parabola is at (h, k).
and the focus of this parabola is at (h, k+a).
From the given,
h = 3, k=5 and k+a = 9
To solve for a;
k+a = 9
Substitute the value of k =5 in above expression:
5+a =9
⇒ a= 9-5 =4
Therefore, the vertex and focus are 4 units apart.
Hence, the equation of parabola by substituting the value of h, k and a in equation [1] ;
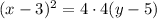 or
or
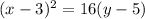 .
.