Question

PLEASE HELP ME!!!! 60 POINTS!!!

Arnold and Jeremy are working on a rocket project for math class. Their job is to find the time it takes for a model rocket to reach its maximum height and how long it will take the rocket to return to Earth if the rocket’s parachute fails to deploy.

They are making calculations for three different rocket engines and each engine has a different initial velocity. They are a bit confused on how to make the calculations. Take a look at the information that they were given and show them how to set up the equations and solve for the times requested.

Answer 1

the first step is look at the answer above this one and copy that

Explanation:

Answer 2

All of these equations will be set up as: h(t) =
`-(g)/(2)t^(2)` +v₀t + h₀ where g represents gravity, v₀ represents initial velocity, and h₀ represents initial height. When working with ft/sec, g = 32. So, -g/2 = -16

1a) Length of time to reach its maximum height means you are looking for the x-value of the vertex (aka Axis Of Symmetry).

h(t) = -16t² + 160t

AOS: x =
`(-b)/(2a)` =
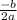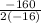`(-160)/(2(-16))` = 5

Answer: 5 sec

1b) Length of time to fall to the ground means you are looking for the x-intercept when height (y-value) = 0.

h(t) = -16t² + 160t

0 = -16t² + 160t

0 = -16t(t - 10)

0 = -16t 0 = t - 10

t = 0 t = 10

t = 0 is when it started, t = 10 is when fell to the ground.

Answer: 10 sec

2c) Same concept as 1a

h(t) = -16t² + 288t

AOS: x =
`(-b)/(2a)` =
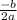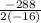`(-288)/(2(-16))` = 9

Answer: 9 sec

2d) Same concept as 1b

h(t) = -16t² + 288t

0 = -16t² + 288t

0 = -16t(t - 18)

0 = -16t 0 = t - 18

t = 0 t = 18

Answer: 18 sec

3e) Same concept as 1a

h(t) = -16t² + 352t

AOS: x =
`(-b)/(2a)` =
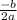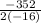`(-352)/(2(-16))` = 11

Answer: 11 sec

3f) Same concept as 1b

h(t) = -16t² + 352t

0 = -16t² + 352t

0 = -16t(t - 22)

0 = -16t 0 = t - 22

t = 0 t = 22

Answer: 22 sec