Question

PLEASE HELP!!!!

Jeremy and Arnold are working on a project for math class in which they are to identify the quadratic equation that represents a rain gauge that sits off the ground. Graph each of the equations and then determine which one could represent the position of the rain catcher that sits above the ground. The x-axis represents the ground.

Answer 1

this is for the other person sorry it wasnt sooner just found this.

Explanation:

Answer 2

NOTES:

Given a quadratic function in standard format (y = ax² + bx + c), the direction of the parabola is as follows:

• if "a" is positive, then opens UP
• if "a" is negative, then opens DOWN

Given a quadratic function in standard format (y = ax² + bx + c), the vertex can be found as follows:

• the Axis Of Symmetry (x-value) is: x =
  `(-b)/(2a)`
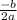
• y-value is found by plugging in the AOS for "x" in the equation

****************************************************************************************

1) y = x² + 11x + 24

• a = +1 so the parabola opens UP

• x =
  `(-b)/(2a)` =
  `(-11)/(2(1))` =
  `-(11)/(2)`

• y =
  `(-(11)/(2))^(2)` + 11
  `(-(11)/(2) )` + 24 =
  `-(25)/(4)`

• vertex
  `(-(11)/(2)`,
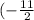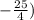  `-(25)/(4))` is in Quadrant 3 and is below the x-axis

This COULD be the graph of the rain gauge.

The graph should contain the vertex, x-intercepts (-3, 0) and (-8, 0), and y-intercept (0, 24)

******************************************************************************************

2) y = -x² - 6x - 8

• a = -1 so the parabola opens DOWN

• x =
  `(-b)/(2a)` =
  `(-(-6))/(2(-1))` =
  `(6)/(-2)` = -3

• y = -(-3)² - 6(-3) - 8 = -9 + 18 - 8 = 1

• vertex (-3, 1) is in Quadrant 2 and is above the x-axis

This could NOT be the graph of the rain gauge.

The graph should contain the vertex, x-intercepts (-2, 0) and (-4, 0), and y-intercept (0, -8)

******************************************************************************************

3) y = x² - 2x + 3

• a = 1 so the parabola opens UP

• x =
  `(-b)/(2a)` =
  `(-(-2))/(2(1))` =
  `(2)/(2)` = 1

• y = (1)² - 2(1) + 3 = 1 - 2 + 3 = 2

• vertex (1, 2) is in Quadrant 1 and is above the x-axis

This could NOT be the graph of the rain gauge.

The graph should contain the vertex, y-intercept (0, 3), and its mirror image (2, 3). There are no x-intercepts

******************************************************************************************

4) y = x² + 4x + 4

• a = 1 so the parabola opens UP

• x =
  `(-b)/(2a)` =
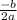  `(-4)/(2(1))` = -2

• y = (-2)² + 4(-2) + 4 = 4 - 8 + 4 = 0

• vertex (-2, 0) is in Quadrant 2 and is on the x-axis

This COULD be the graph of the rain gauge.

The graph should contain the vertex, y-intercept (0, 4), and its mirror image (-4, 4). The x-intercept is the vertex.

Compared to the other four graphs, this is most likely the equation for the rain gauge!

******************************************************************************************

5) y = 3x² + 21x + 30

• a = +3 so the parabola opens UP

• x =
  `(-b)/(2a)` =
  `(-21)/(2(3))` =
  `-(7)/(2)`

• y = 3
  `(-(7)/(2))^(2)` + 21
  `(-(7)/(2) )` + 30 =
  `-(27)/(4)`

• vertex
  `(-(7)/(2)`,
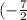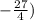  `-(27)/(4))` is in Quadrant 3 and is below the x-axis

This COULD be the graph of the rain gauge.

The graph should contain the vertex, x-intercepts (-2, 0) and (-5, 0), and y-intercept (0, 30)

*******************************************************************************************