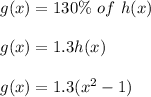Question

The graph of h is a translation 3 units up and 2 units right of the graph of f(x)=x2+4x. For each value of x, g(x) is 130% of h(x). Write a rule for g.

Answer 1

The rule for g is:

`g(x)=1.3(x^2-1)`

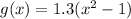
Explanation:

The equation of the function f(x) is given by:

`f(x)=x^2+4x`

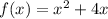
Now, it is given that:

The graph of h is a translation 3 units up and 2 units right of the graph of f(x).

This means that:

`h(x)=f(x-2)+3`

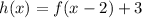
Hence, we have the equation for the function h(x) as:

`h(x)=(x-2)^2+4(x-2)+3\\\\h(x)=x^2+4-4x+4x-8+3\\\\h(x)=x^2+4-8+3\\\\h(x)=x^2-1`

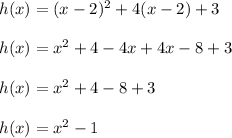
Also, g(x) is 130% of h(x).

i.e.

`g(x)=130\% \ of \ h(x)\\\\g(x)=1.3h(x)\\\\g(x)=1.3(x^2-1)`

Answer 2

We are given

`f(x)=x^2+4x`

h(x):

The graph of h is a translation 3 units up

so, we get

`=x^2+4x+3`

2 units right of the graph of f(x)

so, we get

`h(x)=(x-2)^2+4(x-2)+3`

now, we can simplify it

`h(x)=x^2-4x+4+4\left(x-2\right)+3`

`h(x)=x^2-1`

g(x):

we have

For each value of x, g(x) is 130% of h(x)

so, we get

g(x)=130% of h(x)

`g(x)=(130)/(100) h(x)`

we can plug value

`g(x)=(130)/(100) (x^2-1)`

`g(x)=1.3(x^2-1)`.............Answer