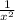Question

Help !!!
See question in image.
Please show workings .
​

Answer 1

see explanation

Explanation:

Given f(x) then the derivative f'(x) is

f'(x) = lim( h tends to 0 )
`(f(x+h)-f(x))/(h)`

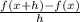
= lim( h to 0 )
`(x+h+(1)/(x+h )-(x+(1)/(x) ) )/(h)`

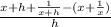
= lim(h to 0)
`(x+h+(1)/(x+h)-x-(1)/(x) )/(h)`

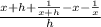
= (lim(h to 0)
`(h+(1)/(x+h)-(1)/(x) )/(h)`

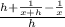
= lim( h to 0 )
`(hx(x+h)+x-(x+h))/(hx(x+h))`

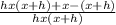
= lim( h to 0 )
`(hx(x+h)+x-x-h)/(hx(x+h))`

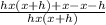
= lim(h to 0 )
`(hx(x+h))/(hx(x+h))` -
`(h)/(hx(x+h))`

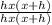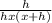
Cancel the numerator/denominator of first fraction and h in the second

= lim ( h to 0 ) 1 -
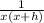`(1)/(x(x+h))` ( let h go to zero ), then

f'(x) = 1 -
`(1)/(x^2)`