Question

Which statement best describes the function below

Answer 1

This is a many to one function (answer C). There are multiple x values that yield the same y.

All of the other statements are wrong. It does not fail the vertical line test and it is definately a function.

Answer 2

The statement which best describes the given function is:

C. It is a many-to-one function.

Explanation:

Function--

A graph is a function if it passes the vertical line test i.e. any line passing through the domain and parallel to y-axis should intersect the curve exactly once.

i.e. corresponding to each element we have just one image.

One-to-one function--

A function is said to be one-to-one if every element has a unique image.

i.e. no two elements have the same image.

Such a function must pass the horizontal line test.

Many-to-one function--

If a function is not one-one i.e. there may be more than one element which have the same image.

We are given a function f(x) by:

`f(x)=2x^2-3x+1`

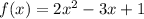
The graph of this function is a upward open parabola ( since the leading coefficient is positive).

Also, the axis of symmetry of function f(x) is:

x=0.75

Since, f(x) is a function this means that it passes the vertical line test.

and it also fails the horizontal line test.

This means that the function is not one-to-one function.

Hence, the function is: Many-to-one function.

( Since, from the figure we have:

x=0 and x=1.5 both have the same image i.e. f(x)=1 )