Question

A hydrogen-like ion is an ion containing only one electron. The energy of the electron in a hydrogen-like ion is given by En = ?(2.18 × 10?18J) Z2 ( 1 n2 ) where n is the principal quantum number and Z is the atomic number of the element. Plasma is a state of matter consisting of positive gaseous ions and electrons. In the plasma state, a mercury atom could be stripped of its 80 electrons and therefore could exist as Hg80+. Use the equation above to calculate the energy required for the last ionization step: Hg79+(g) ? Hg80+(g)+ e?

Answer 1

Answer: Energy required for the ionization of mercury is
`-13.952* 10^(-15)kJ`

Explanation: Energy of the electron in a hydrogen-like ion is given by the equation:

`E_n=((-2.18* 10^(-18))* Z^2)/(n^2)J`

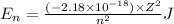
where, Z = atomic number

n = principle quantum number

Ionization energy is the energy required to release the outermost electron from an isolated gaseous atom.

For the ionization of mercury, the equation follows:

`Hg^(79+)\rightarrow Hg^(80+)+e^-`

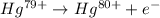
Mercury has an atomic number = 80

As, in this element 79 protons are already released, which means that the electronic configuration for
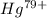`Hg^(79+)` is
`1s^1`

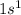
and the principle quantum number for the last ionization step = 1

Putting the values in energy equation, we get

`E_1=((-2.18* 10^(-18))* (80)^2)/((1)^2)J=-13952* 10^(-18)J`

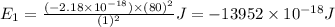
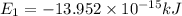`E_1=-13.952* 10^(-15)kJ` (Conversion Factor: 1kJ = 1000J)