(5)
Since, the relationship is linear
so, we can use point slope form of line and find equation of line
we can select any two points
first point is (4,10)
so, x1=4 , y1=10
second point is (7,17.5)
so, x2=7 , y2=17.5
now, we can find slope

now, we can plug values

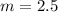
now, we can use point slope form of line

now, we can plug values
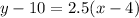
we get
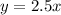
Initial amount:
It is the value of y when x=0
so, we can plug x=0 and find y
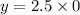
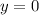
So, initial amount is 0
Rate of change:
we know that rate of change is slope
so, m=2.5
so, the rate of change is 2.5
(6)
Since, the relationship is linear
so, we can use point slope form of line and find equation of line
we can select any two points
first point is (2,29)
so, x1=2 , y1=29
second point is (5,41)
so, x2=5 , y2=41
now, we can find slope

now, we can plug values
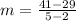
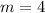
now, we can use point slope form of line

now, we can plug values
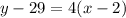
we get
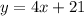
Initial amount:
It is the value of y when x=0
so, we can plug x=0 and find y
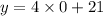
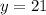
So, initial amount is 21
Rate of change:
we know that rate of change is slope
so, m=4
so, the rate of change is 4