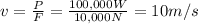Answer:
2. 10 m/s
Step-by-step explanation:
There are two forces acting on the car along the inclined plane:
- The driving force of the car, F, pulling upward along the ramp
- The component of the weight of the car,
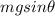 , pulling downward along the ramp
, pulling downward along the ramp
In order to go at constant speed, the acceleration must be zero, so the net force must be zero. Therefore we can write:
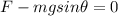
From which we can find the driving force of the car:
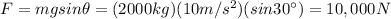
The power of the engine is the product between force and speed of the car:
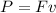
since we know the power,
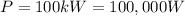 , we can find the speed:
, we can find the speed: