Question

Solve the question below, please

Answer 1

x = 133.33°

Explanation:

The Law of Cosines

It relates the length of the sides of a triangle with one of its internal angles.

Let a,b, and c be the length of the sides of a given triangle, and x the included angle between sides a and b, then the following relation applies:

`c^2=a^2+b^2-2ab\cos x`

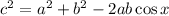
Since we know the values of all three side lengths, we solve the equation for x:

`\displaystyle \cos x=(a^2+b^2-c^2)/(2ab)`

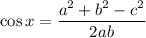
For the triangle in the figure: a=4.1, b=8.5, c=11.7, x=angle C. Applying the formula:

`\displaystyle \cos x=(4.1^2+8.5^2-11.7^2)/(2*4.1*8.5)`

`\displaystyle \cos x=(-47.83)/(69.7)`

`\displaystyle \cos x=-0.6862`

`x = \arccos (-0.6862)`

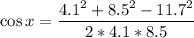
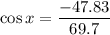
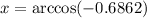
x = 133.33°