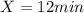Answers:
a) What is the slope and y-intercept and write an equation for this situation?
In order to solve this problem, the figure attached will be helpful.
We already know the initial altitude
 of the balloon in this case is
of the balloon in this case is
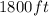 . If we draw a coordinate system (figure attached) where the y-axis represents the altitude of the balloon in feets and the x-axis represents the time in minutes, we will be able to find how the altitude changes with time, in other words the rate of altitude decay of the balloon.
. If we draw a coordinate system (figure attached) where the y-axis represents the altitude of the balloon in feets and the x-axis represents the time in minutes, we will be able to find how the altitude changes with time, in other words the rate of altitude decay of the balloon.
This rate is found by calculating the slope
 of the line that describes the variation of the position in time:
of the line that describes the variation of the position in time:
 (1)
(1)
where
 and
and
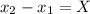
While the equation of the line that describes the movement of the balloon is:
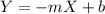 (2)
(2)
where
 is the y-interccept (the point in which the line crosses the y-axis)
is the y-interccept (the point in which the line crosses the y-axis)
Note the negative sign in the equation is because the altitude of the balloon is decreasing, this means the slope is negative. If the line were increasing the equation would be with a positive sign:
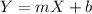 (3)
(3)
Then, according to this the slope is:
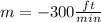 Rate of altitude decay
Rate of altitude decay
Where the negative sign is only to indicate it is decreasing.
Now, if we take
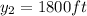 and
and
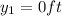 when the balloon finally approaches the ground, and
when the balloon finally approaches the ground, and
 the initial time and
the initial time and
 as the final time, when the balloon is at altitude 0. We will be able to find
as the final time, when the balloon is at altitude 0. We will be able to find
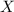 from equation (1), and then the y-intercept from equation (2), by substituting the values we know:
from equation (1), and then the y-intercept from equation (2), by substituting the values we know:
From (1):
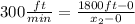
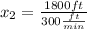
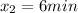 (4)
(4)
Substituting (4) in (2) we will find b or the y-intercept:
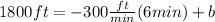

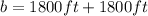
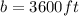 This is the y-intercept
This is the y-intercept
b) Write the equation of the line that models this situation in slope-intercept form:
Here we have to use equation (2), which is also the equation of the line in the slope-intercept form, and substitute the values (
 and
and
 )we calculated above:
)we calculated above:
if
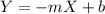
then
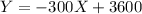
c) How high off the ground is the balloon after 2 minutes?
Here we will use again the equation of the line in the slope-intercept form with the values we calculated and taking into account the following condition:
If
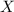 represents the time, then we have to apply the equation (2) when
represents the time, then we have to apply the equation (2) when
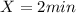 to find the height
to find the height
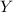 of the balloon after 2 minutes.
of the balloon after 2 minutes.
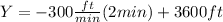

Finally:
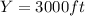
d) How long will it take for air balloon to reach an altitude of 300 feet?
Here we will use the same equation (2), but in this case we want to find the time
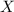 when
when
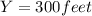 :
:

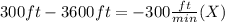

Finally:
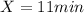
e) How long will it take for the air balloon to land?
If we want to know the answer we will have to use the equation of the line (2) and find
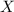 when the height of the balloon is zero, this means
when the height of the balloon is zero, this means
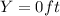 :
:
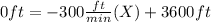
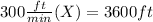
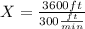
Finally: