Answer:
The measure of angle
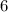 is
is
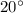
The measure of angle
 is
is
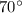
Angles
 and
and
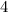 are supplementary
are supplementary
Explanation:
we have that
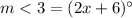
so
For
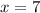

Statements
Verify each statement
see the attached figure to better understand the problem
case A) The measure of angle
 is
is
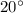
The statement is True
we know that
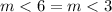 ------> by vertical angles
------> by vertical angles
we have that

so
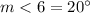
case B) The measure of angle
 is
is
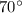
The statement is True
we know that
 ------> by complementary angles
------> by complementary angles
Substitute the value of m<6 and solve for m>5

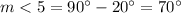
case C) The measure of angle
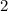 is
is
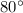
The statement is False
we know that
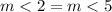 ------> by vertical angles
------> by vertical angles
we have that
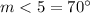
so
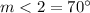
case D) Angles
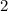 and
and
 are complementary
are complementary
The statement is False
we know that
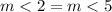 ------> by vertical angles
------> by vertical angles
so
Angles
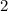 and
and
 are vertical angles and its sum is not equal to
are vertical angles and its sum is not equal to
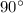
case E) Angles
 and
and
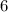 are supplementary
are supplementary
The statement is False
we know that
 ------> by complementary angles
------> by complementary angles
so
Angles
 and
and
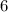 are complementary angles
are complementary angles
case F) Angles
 and
and
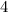 are supplementary
are supplementary
The statement is True
we know that
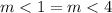 ------> by vertical angles
------> by vertical angles
 ------> by supplementary angles
------> by supplementary angles
Because
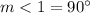 and
and

so
Angles
 and
and
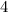 are vertical angles and are supplementary angles
are vertical angles and are supplementary angles