Answer:
The positive value of
 will result in exactly one real root is approximately 0.028.
will result in exactly one real root is approximately 0.028.
Explanation:
Let
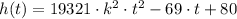 , roots are those values of
, roots are those values of
 so that
so that
 . That is:
. That is:
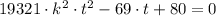 (1)
(1)
Roots are determined analytically by the Quadratic Formula:
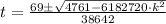
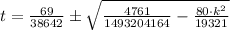
The smaller root is
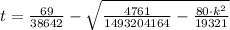 , and the larger root is
, and the larger root is
 .
.
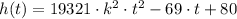 has one real root when
has one real root when
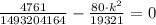 . Then, we solve the discriminant for
. Then, we solve the discriminant for
 :
:
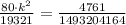
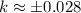
The positive value of
 will result in exactly one real root is approximately 0.028.
will result in exactly one real root is approximately 0.028.