Question

Baking a tray of corn muffins takes 4 cups of milk and 3 cups of wheat flour. Baking a tray of bran muffins takes 2 cups of milk and 3 cups of wheat flour. A baker has 16 cups of milk and 15 cups of wheat flour. He makes $3.00 profit per tray of corn muffins and $2.00 profit per tray of bran muffins. Determine how many trays of each type of muffin the baker should make to maximize his profit.

A. 3 trays of corn muffins and 2 trays of bran muffins
B. 5 trays of corn muffins and 3 trays of bran muffins
C. 4 trays of corn muffins and 2 trays of bran muffins
D. 2 trays of corn muffins and 5 trays of bran muffins

Answer 1

A. 3 trays of corn muffins and 2 trays of bran muffins

Answer 2

Option A.

Explanation:

Let x be the number of trays of corn muffins and y be the number of trays of bran muffins.

He makes $3.00 profit per tray of corn muffins and $2.00 profit per tray of bran muffins.

Objective function: Z=3x+2y

According to the the given information:

Corn muffins Bran muffins Total

Milk 4 2 16

Wheat flour 3 3 15

Subject to the constraints are

`4x+2y\leq 16`

`3x+3y\leq 15`

`x\geq 0,y\geq 0`

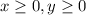
Draw the graph of above qualities as shown below.

The vertices of feasible region are (0,0), (0,5), (3,2) and (4,0).

Point Z=3x+2y

(0,0) 0

(0,5) 10

(3,2) 13

(4,0) 12

The profit is maximum at x=3 and y=2.

3 trays of corn muffins and 2 trays of bran muffins.

Therefore, the correct option is A.