Question

In △ABC point D is the midpoint of AB , point E is the midpoint of BC , and point F is the midpoint of BE . Find area of △ABC, if ADCF= 63 cm2.

Answer 1

For a better understanding of the solution given here please go through the diagram in the file attached.

Let the area of the triangle ABC be denoted by the letter "a".

We know that since D is the midpoint of AB then CD must be a median and we know that a median divides the area of any triangle in half.

Thus, from the figure, Area of
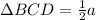`\Delta BCD=(1)/(2)a`....(Equation 1)

Now, in
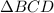`\Delta BCD` DE is the median and thus, Area of
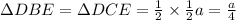`\Delta DBE=\Delta DCE=(1)/(2)*  (1)/(2)a=(a)/(4)`...(Equation 2)

Again, in
`\Delta DBE`, DF is the median, so, area of
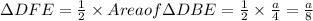`\Delta DFE=(1)/(2)* Area of \Delta DBE=(1)/(2)*  (a)/(4)= (a)/(8)`.......(Equation 3)

As, we can see, the area of the given triangle,
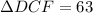`\Delta DCF=63` which is the sum of shaded areas depicted by "x" and "y". Now, this area is obviously, the sum of the area of (Equation 2) and (Equation 3). Thus we have:

`(a)/(4)+ (a)/(8)=63`

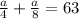
Solving, we get:

`(3a)/(8)=63`

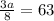
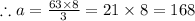`\therefore a=(63* 8)/(3)=21* 8=168` sq cm

Therefore, the required area, that of triangle ABC is 168 squared centimeter.