Question

two right triangles that are not similar still may have one congruent acute angle in common. A. True B. False

Answer 1

Your answer is false.

Answer 2

B.False

Explanation:

We are given that two right angle are not similar and they have one congruent acute angle in common.

We have to tell the statement is false or true.

Suppose two right angles triangle ABC and EFG which are not similar

Let Angle B and angle F are of 90 degrees

One acute angle common in two triangles

Suppose that angle C=angle G=x, angle A=y, angle E=z

In right angled triangle ABC

`m\angle A+m\angle B+m\angle C=180^(\circ)`

`x+y+90=180^(\circ)`

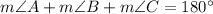
In right angled triangle EFG

`m\angle E+m\angle F+m\angle G=180^(\circ)`

`z+x+90=180^(\circ)`

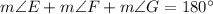
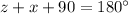
Substitute the values equal then we get

`x+y+90=z+x+90`

`x+y+90-x-90=z`

`y=z`

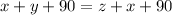
Hence, all three angles of a right triangle are similar to all three corresponding angles of another right angled triangle.

Therefore, the two triangles must be similar by AAA similarity postulates.

Hence, the statement is false.