Question

Suppose the path of a golf ball in a chip shot from a small hill, follows the path graphed by the quadratic function f(d)= -1.6d^2+3.3d+0.2 where d is the horizontal distance the ball travels, and the f(d) is the height, in meters, of the ball at d horizontal meters. Find the maximum height of the ball and the horizontal distance the ball traveled to reach its maximum height.

A. Maximum height: 1.03 meters, to reach maximum height: 1.90 meters horizontally

B. Maximum height: 0.2 meters, to reach maximum height: 1.03 meters horizontally

C. Maximum height: 1.90 meters, to reach maximum height: 1.03 meters horizontally

D. Maximum height: 1.03 meters, to reach maximum height: 1.6 meters horizontally

Answer 1

The quadratic function f(d)= -1.6d^2+3.3d+0.2 represents parabola.

Find the vertex of this parabola:

1. the d-coordinate of the parabola is

`d_v=-(b)/(2a)=-(3.3)/(2\cdot (-1.6))=(3.3)/(3.2)=(33)/(32)\approx 1.03\ m.`

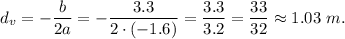
2. the f(d)-coordinate of the parabola is

`f(d_v)=-1.6\cdot (1.03)^2+3.3\cdot 1.03+0.2\approx 1.90\ m.`

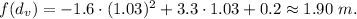
Therefore maximal vertical height is 1.90 meters and to reach maximal height the ball should travel 1.03 m horizontally.

Answer: correct choice is C