Question

Katherine is shopping for cupcakes and donuts. She can purchase at most 30 items in total. She also wants the number of cupcakes purchased to be greater than or equal to the square of 2 more than the number of donuts.

Create a system of inequalities to model the above situation and use it to determine how many of the solutions are viable.

Answer 1

Part of the solution region includes a negative number of donuts purchased; therefore, not all solutions are viable for the given situation.

Explanation:

Answer 2

Let the number of cupcakes be represented by = y

Let the number of donuts be represented by = x

She can purchase at most 30 items in total so equation becomes:

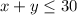`x+y\leq30` .... (1)

She also wants the number of cupcakes purchased to be greater than or equal to the square of 2 more than the number of donuts. Hence, equation becomes:

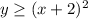`y\geq(x+2)^(2)` ....(2)

The intersection point where value of 'x' is negative is not valid.

Hence, points 3 and 27 is the answer. (rounding off 3.179 and 26.821)

Please find attached the graph.