Answer:
x=32
Explanation:
We are given that a triangle XYZ in which
XY=YZ=ZY
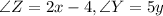
We have to find the value of x.
We know that when all sides of triangle are equal then, the triangle is equilateral triangle and each angle of equilateral triangle is equal to 60 degrees.
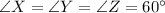
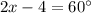
Using substitution property of equality
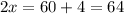
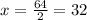
Hence, the value of x=32