Question

Simplify 
(−3 + i) / (7+i)

Answer 1

Answer: -2/5+1/5i

Explanation:

complex rule.

(-3*7+1*1)+(1*7-(-3)*1)i/7²+1² ← as the fractions

then refine and rewrite the problem down.

-20+10i/50 ← as the fractions shown.

-20+10i/50=-2+i/5

you can also rewrite the problem down in standard complex form.

-2+i/5=-2/5+1/5i

=-2/5+1/5i

Hope this helps!

Thanks!

Have a great day!

Answer 2

Begin by observing the conjugate of 7 + i The conjugate has the same real part (7) in this case and the opposite sign for the complex part.

... The conjugate is 7 - i

The next thing to do is multiply the numerator and denominator by the confugate.

`\text{...}(-3 + i )/(7 + i)*(7 - i)/(7 - i)`

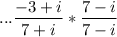
You have 2 fractions that you must multiply together. You do it by numerator times numerator and denominator * denominator.

... numerator: (-3 + i) (7 - i ) = -21 + 3i + 7i - i^2 = -21 + 10i - i^2 = -21 + 10i + 1

... numerator: -20 + 10i

... denominator: (7 + i)(7 - i) = 49 - 7i + 7i - i^2 = 49 - i^2 = 50

Next you divide the numerator by the denominator.

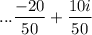`\text{...}(-20)/(50) + (10i)/(50)` Reduce

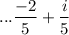`\text{...}(-2)/(5) + (i)/(5)` Answer