Question

Identify the vertical asymptote and the hole on the graph of the function f(x) = x2+x-6/x2-6x+8.  ANSWER:

There is an asymptote at x=__.         --> 4
There is a whole at (__,__).               --> (2,2.5)

Answer 1

2

4

-2.5

Explanation:

Answer 2

The vertical asymptote is x=4. The function has whole at x=2.

Explanation:

The given function is

`f(x)=(x^2+x-6)/(x^2-6x+8)`

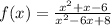
Find factor form of numerator and denominator.

`f(x)=(x^2+3x-2x-6)/(x^2-4x-2x+8)`

`f(x)=(x(x+3)-2(x+3))/(x(x-4)-2(x-4))`

`f(x)=((x+3)(x-2))/((x-4)(x-2))`

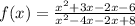
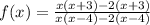
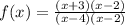
Cancel out the common factors.

`f(x)=(x+3)/(x-4)`

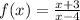
Now equate the denominator equal to 0, to find the vertical asymptote.

`x-4=0`

`x=4`

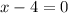
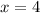
The vertical asymptote is x=4.

Equate the cancel factor equal to zero to find the whole.

`x-2=0`

`x=2`

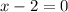
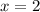
The function has whole at x=2.

At whole, the value of function is undefined but limit of the function exist.

`f(2)=(2+3)/(2-4)=-2.5`

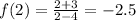
Therefore the limit of the function at x=2 is -2.5.