Question

How do you do complete the square with circle in center radius form

Answer 1

we know that formula of circle in standard form

`(x-h)^2+(y-k)^2=r^2`

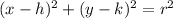
where

(h,k) is center of circle

r is radius of circle

Here , we can see that (x-h)^2 and (y-k)^2 are perfect squares

so, we will change our equations in perfect square

For example:

`x^2+y^2+16x-14y+49=0`

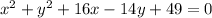
Firstly, we will change x terms into perfect square

step-1:

we will move constant term on right side

`x^2+y^2+16x-14y+49-49=0-49`

`x^2+y^2+16x-14y=-49`

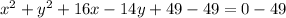
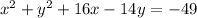
step-2:

We will move all x terms altogether

`x^2+16x+y^2-14y=-49`

step-3:

Break x terms as 2*a*b

`x^2+2* 8* x+y^2-14y=-49`

step-4:

now, we can use formula

`a^2+2ab+b^2=(a+b)^2`

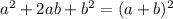
we will identify b

so, we get b=8

to make 8^2 , we will add both sides by 8^2

`x^2+2* 8* x+8^2+y^2-14y=-49+8^2`

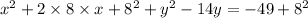
now, we can write in perfect square form

`(x+8)^2+y^2-14y=15`

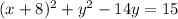
step-5:

now, we can break y terms in 2ab form

`(x+8)^2+y^2-2* 7* y=15`

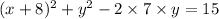
step-6:

now, we can use formula

`a^2-2ab+b^2=(a-b)^2`

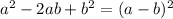
we will identify b

so, we get b=7

to make 7^2 , we will add both sides by 7^2

`(x+8)^2+y^2-2* 7* y+7^2=15+7^2`

`(x+8)^2+(y-7)^2=64`

`(x+8)^2+(y-7)^2=8^2`

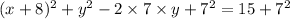
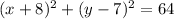
we can see that this is in standard equation of circle form

so, center=(-8,7)

radius=8