Answer:
Parallel line A :

Perpendicular to line A :
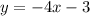
Neither parallel nor perpendicular to line A :
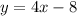
Explanation:
The equation of line A is
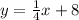 ... (1)
... (1)
The slope intercept form of a line is
 .... (2)
.... (2)
where, m is slope and b is y-intercept.
From (1) and (2) we get

It means the slope of line A is 1/4.
The slope of parallel lines are same and the product of slopes of two perpendicular lines is -1.
In equation
 , the slope is 1/4 which is same as slope of line A. So, line
, the slope is 1/4 which is same as slope of line A. So, line
 is parallel to line A.
is parallel to line A.
In equation
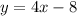 , the slope is 4 which not equal to slope of line A and
, the slope is 4 which not equal to slope of line A and
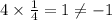 . So, line
. So, line
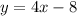 is neither parallel nor perpendicular to line A.
is neither parallel nor perpendicular to line A.
In equation
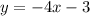 , the slope is -4 which is not equal to the slope of line A and
, the slope is -4 which is not equal to the slope of line A and
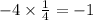 . So, line
. So, line
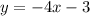 perpendicular to line A.
perpendicular to line A.