Given function:
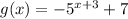
We need to find the correct graph in the given options.
In order to find the correct, we need to find the x-intercept.
In order to find the x-intercept, we need to put given function equal to 0 and then solve for x.
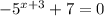
Subtracting 7 from both sides, we get
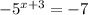
Dividing both sides by -1, we get
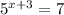
Taking ln on both sides, we get
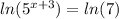
(x+3)

Dividing both sides, by ln(5), we get
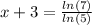
x+3 =1.21
x= 1.21 -3
x=-1.79.
From the given options, we can see the 4th option has x-intercept at -1.79.
Therefore, 4th option is correct option.