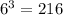Answer:
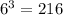
Explanation:
The expression is
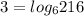
To transform this logarithm in exponential form, we have to use the definition that relates both functions,
Where the base of the logarithm is the base of the exponential form.
The result of the logarithm is the exponent of the exponential form.
And the argument of the logarithm is the result of the exponential expression.
Now, applying the transformation, we have:

Therefore, the equivalent exponential form is