1 Answer

Zegnus · Answer 1 · 2019-11-17T19:33:57+0000

Answer: The correct option is B.

Step-by-step explanation:

The given inequalities are,

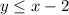
$y\leq x-2$

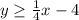
$y\geq (1)/(4)x-4$

The relative equation of (1) inequality is,

y= x-2

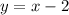
At x=0, we get y=-2 and x=1, we get y=-1.

Check the first inequality by origin (0,0).

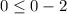
$0\leq 0-2$

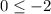
$0\leq -2$

This statement is false therefore the the point (0,0) not lies in the shade area of
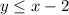$y\leq x-2$ .

The relative equation of (2) inequality is,

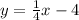
y=(1)/(4)x-4

At x=0, we get y=-4 and x=4, we get y=-3.

Check the first inequality by origin (0,0).

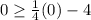
$0\geq (1)/(4)(0)-4$

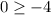
$0\geq -4$

This statement is true therefore the the point (0,0) will lies in the shade area of
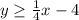$y\geq (1)/(4)x-4$ .

From the graph we can say that the common shade region is B.

Please log in or register to add a comment.