Question

Why is the sum of two rational numbers always rational? Select from the drop-down menus to correctly complete the proof.

Let a/b and c/d represent two rational numbers. This means a, b, c, and d are , and . The sum of the numbers is ad+bc bd , where bd is not 0. Because integers are closed under , ​the sum is the ratio of two integers, making it a rational number.

Answer 1

when adding you always get a rational number because you never go outside the bounds of reality XD

Answer 2

Explanation:

The complete question is:

Why is the product of two rational numbers always rational? Select from the Bold words to correctly complete the proof.

Let ab and cd represent two rational numbers. This means a, b, c, and d are (Integers or irrational numbers), and (b is not 0, d is not 0 or b and d are 0). The product of the numbers is acbd, where bd is not 0. Because integers are closed under (addition or multiplication), ​acbd ​ is the ratio of two integers, making it a rational number.

The correct paragraph would be:

Let
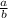`(a)/(b)` and
`(c)/(d)` represent two rational numbers. This means a, b, c, and d are integers (because rational numbers are formed by integers, we could say that they are the ratio between two integers), and b is not 0 and d is not 0 (b and d can't be zeros, because they are denominator, and a rational number with zero denominator is undefined or undetermined, infinite would say). The product of the numbers is
`(a)/(b) * (c)/(d)`, where bd is not 0. Because integers are closed under multiplication (the product of two rational numbers actually is defined as the close up of two integers multiplication, numerators with numerators and denominator with denominator, and always the denominator product cannot be zero), ​acbd ​ is the ratio of two integers, making it a rational number.