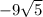Question

What is −2√20 − √125 in simplest radical form? Enter your answer in the box.

Answer 1

`-9√(5)`

Step-by-step explanation:

We have:

`-2√(20) -√(125)`

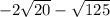
Now, we need to transform each sub-radical number in another pair of numbers that allow us to simplify each radical into a common radical.

So, we know that 20=4(5), and 125=25(5).

Replacing these in the expression:

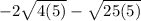`-2√(4(5))-√(25(5))`; but 4 and 25 have squared roots.

Then:

`-2(2)√(5) -5√(5)\\ -4√(5)-5√(5)`

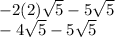
Now, we can operate these terms, because they are like terms, that is, they have the same root. Therefore, the simplest radical form is:

`-9√(5)`

Answer 2

The simplified form of the radical expression is
`-9\sqrt5`

Step-by-step explanation:

We have been given the radical expression
`-2√(20)-√(125)`

First of all, we find the factors of 20 and 125

`20=4 * 5\\\\125 = 25 * 5`

On plugging these values in the given expression, we get

`-2√(4 * 5)-√( 25 * 5)`

We know that square root of 4 is 2 and square root of 25 is 5. Hence, we have

`2* 2 \sqrt 5 - 5\sqrt 5\\\\-4\sqrt5 - 5\sqrt 5\\\\-9\sqrt5`

Therefore, the simplified form of the radical expression is
`-9\sqrt5`