Question

Find the coordinates of the circumcenter for ∆DEF with coordinates D(1,3) E (8,3) and F(1,-5). Show your work.

Answer 1

Answer: The coordinates of the circumcenter is
`((9)/(2), -1)`.

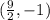Step-by-step explanation:

The coordinates of triangle DEF are D(1,3) E (8,3) and F(1,-5).

Distance formula,

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

`DE=√((8-1)^2+(3-3)^2)=7`

`FE=√((1-8)^2+(-5-3)^2)=√(7^2+8^2)`

`DF=√((1-1)^2+(-5-3)^2)=8`

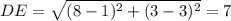
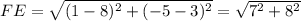
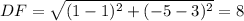
Since triangle follows pythagoras theorem,

`(DF)^2+(DE)^2=(FE)^2`

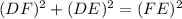
Therefore the given triangle is a right angle triangle.

Or plot these points on a coordinate plane. From the figure we can say that the triangle DEF is a right angle triangle.

The circumcenter of a right angle triangle is the midpoint of the hypotenuse.

The hypotenuse is EF. The midpoint of EF is,

`Midpoint =((8+1)/(2), (3-5)/(2) )=((9)/(2), -1)`

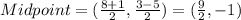
Therefore, the coordinates of the circumcenter is
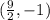`((9)/(2), -1)`.