1 Answer

MKroeders · Answer 1 · 2019-09-30T12:57:39+0000

Answer-

The maximum area that they can fence off is 6400 ft²

Solution-

Organizers of an outdoor concert will use 320 feet of fencing to fence off a rectangular vip section.

i.e the perimeter of the rectangular section is 320 feet

Let us assume,

x = length of the rectangular section

y = breadth of the rectangular section

Hence,

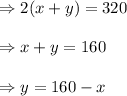
$\Rightarrow 2(x+y)=320\\\\\Rightarrow x+y=160\\\\\Rightarrow y=160-x$

Now, we have to find the maximum area for which they can fence that off.

The area of the rectangular section is,

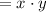
$=x\cdot y$

So we have to maximize the area function.

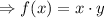
$\Rightarrow f(x)=x\cdot y$

Putting the value of y,

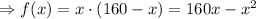
$\Rightarrow f(x)=x\cdot (160-x)=160x-x^2$

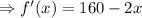
$\Rightarrow f'(x)=160-2x$

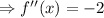
$\Rightarrow f''(x)=-2$

Finding the critical values,

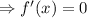
$\Rightarrow f'(x)=0$

$\Rightarrow 160-2x=0$

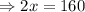
$\Rightarrow 2x=160$

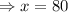
$\Rightarrow x=80$

∵ f"(x) is negative (i.e -2), so for the value of x=80, f(x) or area function will be maximum.

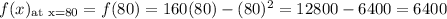
$f(x)_{\text{at x=80}}=f(80)=160(80)-(80)^2=12800-6400=6400$

Therefore, the maximum area that they can fence off is 6400 ft²

Please log in or register to add a comment.