Question

Please help me. its attached

Answer 1

5. ΔABC ≅ ΔDEF is true.

6. ΔABC ≅ ΔGHI is not true.

Step by step explanation

5. Find the lengths of the triangle ABC.

BC = 3

Use the distance formula to find the length of AB and AC

Distance formula =
`√((x2 - x1)^2 + (y2 - y1)^2)`

Coordinates of A = (1, 4) and B = (2, 2).

Now plug in these values in to the distance formula.

AB =
`√((2 -1)^2 + (2 - 4)^2) \\`

AB =
`√((1)^1 + (-2)^2)`

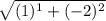
AB = √1 + 4

AB = √5

Now let's find the length of AC.

A = (1, 4), C = (5, 2)

Use the distance formula and the length of AC.

AC =
`√((5 - 1)^2 +(2 - 4)^2)`

AC =
`√((4)^2 + (-2)^2)`

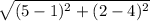
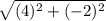
AC = √(16 + 4)

AC = √20

Now let's find the length of GI

G = (6, 6) and I = (8, 1)

Use the distance formula.

GI = √(2)^2 + (-5)^2

GI = √(4 + 25)

GI = √29.

The length of EF = 3, DE = √5, EF = √20

Now let's compare the two triangles ABC and DEF.

The sides of the triangle ABC is equal to the sides of the triangle DEF

By SSS property, ΔABC ≅ ΔDEF.

6) The side length of GI = √29 which is not equal to the side length of AC = √20.

Therefore, the ΔABC ≅ ΔGHI is not true.

Hope this will help you.

Thank you.