Question

Please help and Imma be postin these all night I literally suck at algebra two so just check my profile if your good at math :)

Answer 1

The range of the equation is y ≥ 9 ⇒ C

Explanation:

The quadratic equation y = ax² + bx + c, represents by a parabola of vertex (h, k), where h =
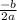`(-b)/(2a)` and k is the value of y at x = h

• The range of the quadratic if it has a minimum vertex is y ≥ k, and y ≤ k if it has a maximum vertex

• The parabola has a minimum vertex if the value of a is positive and a maximum vertex if the value of a is negative

∵ The equation is y = x² + 9

→ Compare it with the form above to find a and b

∴ a = 1 and b = 0

∵ a is a positive number

∴ The parabola has a minimum vertex

→ By using the 1st rule above

∴ The range is y ≥ k

→ Use the rule of h above to find it

∵ h =
`(-(0))/(2(1))` =
`(0)/(2)`

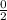
∴ h = 0

→ To find k substitute x by the value of h and y by k

∵ k = (0)² + 9

∴ k = 0 + 9

∴ k = 9

∴ The range of the equation is y ≥ 9