Given vertices of the rectangle :
(-2,8)
(4,9)
(6,-3) and (0,-4)
Length of the rectangle is the distance of (-2,8) to (4,9).
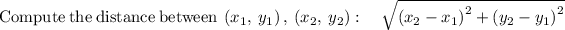
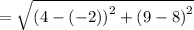
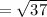
Width of the rectangle is the distance of (4,9) and (6,-3).
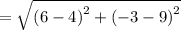
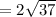
Area of the rectangle = Length × Width
=
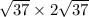
= 2 × 37
= 74.
Therefore, area of the rectangle is 74 units².