Question

My question is on the image it would mean the world to me if you could help

Answer 1

a. Slope of f(x) is greater than g(x)

b. y-intercept of f(x) is less than the y-intercept of g

Explanation:

Function f(x)

Given the function f(x)

x f(x)

-3 -0.5

-2 0

-1 0.5

0 1

Finding the slope between any two points

`\mathrm{Slope}=(y_2-y_1)/(x_2-x_1)`

`\left(x_1,\:y_1\right)=\left(-3,\:-0.5\right),\:\left(x_2,\:y_2\right)=\left(-2,\:0\right)`

`m=(0-\left(-0.5\right))/(-2-\left(-3\right))`

`m=0.5`

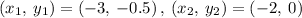
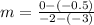
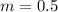
Thus,

The slope of f(x) = 0.5

We know that the value of the y-intercept can be determined by setting x = 0, and determining the corresponding value of y.

From the given point (0, 1), we can easily observe that at x = 0, the value of y = 1.

Thus, the y-intercept of f(x) = 1

Function g(x)

Taking two points from the given graph of g(x)

• (1, 0)

• (0, 2)

Finding the slope between (1, 0) and (0, 2)

`\mathrm{Slope}=(y_2-y_1)/(x_2-x_1)`

`\left(x_1,\:y_1\right)=\left(1,\:0\right),\:\left(x_2,\:y_2\right)=\left(0,\:2\right)`

`m=(2-0)/(0-1)`

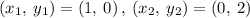
Refine

`m=-2`

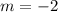
Thus,

The slope of g(x) = -2

We know that the value of the y-intercept can be determined by setting x = 0, and determining the corresponding value of y.

From the given point (0, 2), we can easily observe that at x = 0, the value of y = 2.

Thus, the y-intercept of g(x) = 2

Conclusion:

FOR function f(x)

The slope of f(x) = 0.5

The y-intercept of f(x) = 1

FOR function gx)

The slope of g(x) = -2

The y-intercept of g(x) = 2

Thus:

a. Slope of f(x) is greater than g(x)

b. y-intercept of f(x) is less than the y-intercept of g