Question

Enter the number of complex zeros for the polynomial function in the box.

f(x)=x^3−96x^2+400

Answer 1

Given polynomial function:

`f(x)=x^3-96x^2+400`.

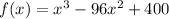We need to apply Descartes' rule of sign to identify the number of complex roots.

The given polynomial is f(x)=x^3-96x^2+400

Let us see the number of sign changes in f(x)

There are 2 sign changes in f(x). One from plus to minus and second from plus to minus. Hence, there 2 or 0 positive roots.

Now, let us see the number of sign changes in f(-x)

f(-x)=-x^3-96x^2+400

There are only one sign change. Hence, there will be 1 negative roots.

The degree of the polynomial is 3.

Hence, there will be exactly 3 zeros.

Therefore, the possible numbers of zeros are:

2 positive, 1 negative and 0 complex

0 positive, 1 negative and 2 complex.

Let us see the graph:

In the graph, we can see that the graph cuts the x axis at three points (2 positive, 1 negative points).

Hence, the number of complex zeros for the given polynomial is zero.