Question

Explain why any of the four operations placed between two terms 5 and -3 sqrt (8) will result in an irrational number

Answer 1

Sum/difference:

Let

`x = 5 + (-3√(8)) = 5-3√(8)`

This means that

`3√(8) = 5-x \iff √(8) = (5-x)/(3)`

Now, assume that
`x` is rational. The sum/difference of two rational numbers is still rational (so 5-x is rational), and the division by 3 doesn't change this. So, you have that the square root of 8 equals a rational number, which is false. The mistake must have been supposing that
`x` was rational, which proves that the sum/difference of the two given terms was irrational

Multiplication/division:

The logic is actually the same: if we multiply the two terms we get

`x = -15√(8)`

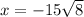
if again we assume x to be rational, we have

`√(8) = -(x)/(15)`

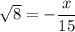
But if x is rational, so is -x/15, and again we come to a contradiction: we have the square root of 8 on one side, which is irrational, and -x/15 on the other, which is rational. So, again, x must have been irrational. You can prove the same claim for the division in a totally similar fashion.