Question

Plz help meee 2 more problems and I am done

Answer 1

Explanation:

Figure 1,

EA and EB are the opposite rays.

EC bisects angle FEG.

a). m∠FEC =
`(1)/(2)(m\angle FEG)`

(2x + 6) =
`(1)/(2)(40)`

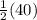
2x + 6 = 20

2x = 14

x = 7

b). ED⊥AB

Therefore, m∠AED = 90°

m∠AED = 11y + 13 = 90°

11y = 90 - 13

11y = 77

y = 7

Figure 2,

NC bisects ∠WNB,

Therefore, ∠WNC ≅ ∠CNB

m∠WNC = m∠CNB

3v - 4 = 2v + 6

3v - 2v = 4 + 6

v = 10

Therefore, m∠WNC = x = (3v - 4)

x = 3(10) - 10

= 30 - 10

x = 20