Question

A candle burned at a steady rate. After 38 minutes, the candle was 11.2 inches tall. Eighteen minutes later, it was 10.75 inches tall. Use an equation in point-slope form to determine the height of the candle after 4 hours. Round the answer to the tenth place if necessary.

Answer 1

To determine the height of the candle after 4 hours, we can use the point-slope form of a linear equation. The equation relating time and height of the candle is y - 11.2 = -0.00278(x - 38). To find the height after 4 hours, substitute x = 240 into the equation.

Step-by-step explanation:

To solve this problem, we can use the point-slope form of a linear equation. We know that the height of the candle decreases linearly over time. Let's use the two given points: (38, 11.2) and (38+18, 10.75) to find the equation.

First, let's find the slope using the formula:

slope = (y2 - y1) / (x2 - x1) = (10.75 - 11.2) / (38+18 - 38) = -0.05 / 18 = -0.00278

Next, we can use the point-slope form:

y - y1 = m(x - x1)

Substituting the values (x1, y1) = (38, 11.2) and m = -0.00278, we have:

y - 11.2 = -0.00278(x - 38)

Now, to find the height of the candle after 4 hours (240 minutes), substitute x = 240 into the equation and solve for y.

Answer 2

Let us take time by x variable and height of the candle by y variable.

We can setup two coordinates form the given statements:

After 38 minutes, the candle was 11.2 inches tall : (38, 11.2)

Eighteen minutes later, it was 10.75 inches tall : (56,10.75).

We need to write slope -intercept form of the equation first.

Slope-intercept form is :

y-y1 = m(x-x1).

In order to find slope-intercept form we need to find the slope of the given equation.

Slope between (38, 11.2) and (56, 10.75) points :

`m=(10.75-11.2)/(56-38)`

`m=-0.025`

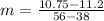
Let us apply slope-intercept form y-y1 = m(x-x1).

y- 11.2 = -0.025 (x-38)

Now, we need to find the height of the candle after 4 hours.

We took time in minutes.

Therefore, 4 hours = 4× 60 = 240 minutes.

In order to find the height of the candle after 4 hours, we need to plug x=240 in above slope-intercept form.

y- 11.2 = -0.025 (240-38)

y-11.2 = -0.025 ( 202)

y-11.2 = -5.05

Adding 11.2 on both sides, we get

y-11.2+11.2 = -5.05+11.2

y = 6.15

We need to round it to the tenth place.

Therefore, y = 6.15.

Therefore, the height of the candle after 4 hours is 6.15 inches.