Answer:
a) A force of 367718.75 newtons is needed to get the full airplane safely in the air.
b) The empty airplane would need a runway of 1828.571 meters.
Step-by-step explanation:
a) This problem can be solved by using the Work-Energy Theorem, which states that work needed by the airplane to get minimum speed is equal to its change in translational kinetic energy, both measured in joules. The resulting formula is presented below:
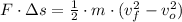 (1)
(1)
Where:
 - Minimum net force, measured in newtons.
- Minimum net force, measured in newtons.
 - Runway length, measured in meters.
- Runway length, measured in meters.
 - Mass of the airplane, measured in kilograms.
- Mass of the airplane, measured in kilograms.
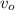 ,
,
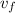 - Initial and final speeds of the airplane, measured in meters per second.
- Initial and final speeds of the airplane, measured in meters per second.
If we know that
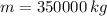 ,
,
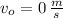 ,
,
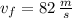 and
and
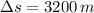 , then the minimum net force needed by the airplane to get itself safely in the air:
, then the minimum net force needed by the airplane to get itself safely in the air:
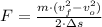
![F = ((350000\,kg)\cdot \left[\left(82\,(m)/(s) \right)^(2)-\left(0\,(m)/(s) \right)^(2)\right])/(2\cdot (3200\,m))](https://img.qammunity.org/2022/formulas/physics/high-school/zwo4fuoeesdrg5bhfwmiyz3tooydth41n9.png)

A force of 367718.75 newtons is needed to get the full airplane safely in the air.
b) If we know that
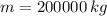 ,
,
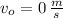 ,
,
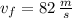 and
and
 , then the length of the runway is:
, then the length of the runway is:
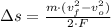
![\Delta s = ((200000\,kg)\cdot \left[\left(82\,(m)/(s) \right)^(2)-\left(0\,(m)/(s) \right)^(2)\right])/(2\cdot (367718.75\,N))](https://img.qammunity.org/2022/formulas/physics/high-school/3hc5y9htjor12h44k4yghmx543ndesv2fp.png)
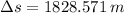
The empty airplane would need a runway of 1828.571 meters.