Question

Find the equation of the axis of symmetry and the coordinates of the vertex of the graph of the function:

y =2x2+12x+13

Answer 1

Given equation: y =2x^2+12x+13.

We need to find the axis of symmetry and the coordinates of the vertex of the graph of the function.

The formula of axis of symmetry is :
`-(b)/(2a)`.

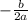a= 2 and b=12.

Therefore,
`-(b)/(2a) = -(12)/(2(2))  = -(12)/(4) = -3`.

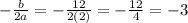Therefore, axis of symmetry is x=-3.

Let us find y-coordinate of the vertex.

Plugging x=-3 in given quadratic y =2x^2+12x+13.

y= 2(-3)^2+12(-3)+13 = 2(9) -36 +13 = 18-36 +13 = -5.

We got x-coordinate of the vertex -3 and y-coordinate of the vertex -5.

Therefore, vertex of the graph is (-3,-5).