Question

HOW DO YOU FIND THE SINE, COSINE, AND TANGENT VALUES GIVEN A POINT ON A CIRCLE? BE ABLE TO PROVIDE AN EXAMPLE

Answer 1

Given that a point is marked on the unit circle say it is
`\left((1)/(2),(√(3))/(2)\right)`

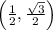
That meanns base of the triangle

`AB=(1)/(2)`

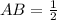
and hight of the right angle triangle

`BC=(√(3))/(2)`

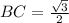
Since it is unit circle so automatically AC=1

or you can use Pythagorean theorem to find side AC.

Now we can use ratios of sine, cos and tan to find their values as follows:

`\sin\left(A\right)=(Perpendicular)/(Hypotenuse)=(BC)/(AC)=((√(3))/(2))/(1)=(√(3))/(2)`

`Cos\left(A\right)=(Base)/(Hypotenuse)=(AB)/(AC)=((1)/(2))/(1)=(1)/(2)`

`\tan\left(A\right)=(Perpendicular)/(Base)=(BC)/(AB)=((√(3))/(2))/((1)/(2))=√(3)`

Same way you can find values of sin, cos, tan etc for any given point on the circle.